Further Mechanics | Chapter 4: Rotation of a rigid body

Curriculum Objectives

• understand and use the definition of the moment of inertia of a system of particles about a fixed axis as $\sum {m{r^2}} $ and the additive property of moment of inertia for a rigid body composed of several parts (the use of integration to find moments of inertia will not be required); 
• use the parallel and perpendicular axes theorems (proofs of these theorems will not be required); 
•  recall and use the equation of angular motion $C = I\ddot \theta $ for the motion of a rigid body about a fixed axis (simple cases only, where the moment C arises from constant forces such as weights or the tension in a string wrapped around the circumference of a flywheel; knowledge of couples is not included and problems will not involve consideration or calculation of forces acting at the axis of rotation); 
• recall and use the formula ${\textstyle{1 \over 2}}I{\omega ^2}$ for the kinetic energy of a rigid body rotating about a fixed axis;
•  use conservation of energy in solving problems concerning mechanical systems where rotation of a rigid body about a fixed axis is involved.

Note:

The following chapter is going to involve angular and linear acceleration and velocity. The notation used up till now has been such that linear velocity and acceleration are given by the Latin alphabets, v and a, while the angular counterparts have been denoted by Greek alphabets, $\omega $ and $\alpha $. There is an alternate notation that is given precedence by many, including it seems your examiners. This notation uses concept of differentiation. We begin by fixing the following convention: the linear displacement is given by s; the angular displacement is given by $\theta $; and the time-derivative (the differentiation of a function with respect to time) of is denoted by a dot on the top. With this convention in place linear velocity becomes $\dot s$, linear acceleration becomes $\ddot s$, angular velocity $\dot \theta $, and the angular acceleration is given $\ddot \theta $

Moment of Inertia

Imagine a body being rotated around an axis, O, and further imagine a point, P, on it, such that the distance from O is given by ${r_i}$, its mass by ${m_i}$, and the its velocity is given by ${v_i}$. You should recall from your previous work on classical mechanics that the kinetic energy of the particle is given by ${\textstyle{1 \over 2}}{m_i}{v_i}^2$. From the work that we have done up till now, we know that ${v_i} = {r_i}\omega $ where $\alpha $ is the angular velocity of the particle. Thence we deduce that the Kinetic Energy of that single particle is ${\textstyle{1 \over 2}}{m_i}{\left( {{r_i}\omega } \right)^2} = {\textstyle{1 \over 2}}{m_i}{r_i}^2{\omega ^2}$.

If we now model that body as a collection, or matrix, of such points, then the total rotational kinetic energy for the body is given by: 

\[\sum {{\textstyle{1 \over 2}}{m_i}{r_i}^2{\omega ^2}} \]

As ${\textstyle{1 \over 2}}$ is a constant and so is angular acceleration, we can say that:

\[Total\,Rotational\,Kinetic\,Energy = {\textstyle{1 \over 2}}\left( {\sum {{m_i}{r_i}^2} } \right){\omega ^2} = {\textstyle{1 \over 2}}I{\omega ^2} \]

If we compare this with its linear counterpart, under the pretence that these are similar formulae, we can see that the role of linear velocity is played by its angular counterpart, and that role of mass is played by ${\sum {{m_i}{r_i}^2} }$. This quantity is particularly important in our study. To see how it is important we shall draw parallels from mass in the Linear Kinetic Energy formula. The mass (of an object) can be understood to a measure of inertia, or the ability of the body to oppose changes in its state of motion. Which is to say that you will require a greater amount of force to cause the same acceleration (or impart the same amount of velocity) to a more massive body. Think how it easier for you to push a toddler than a full grown man. In rotational motion that we are dealing with here, not only the mass but the distance between the particle is also important to that particles inertia, because as you will come to see a particle at a greater distance to the origin will require more torque to be applied to it, than a particle of same mass that is closer to cause the same measure of angular acceleration. Hence the quantity, ${{m_i}{r_i}^2}$, is the rotational inertia of the particle P, and ${\sum {{m_i}{r_i}^2} }$, is the rotational inertia of the entire body. We call this quantity the moment of inertia.

\[I = \sum {{m_i}{r_i}^2} \]

The SI unit of this quantity is \[kg\,{m^2}\]

The Equation of Rotational Motion

For an object in rotational motion, we have the following equation. The derivation of this is not particularly difficult, though it does require a result we haven't yet used. For this reason and that it is not required by your board the proof is put in the relevant post and you need only note the following:

\[C = I\ddot \theta \]

or alternatively you may note:

\[\tau  = I\alpha  \]

The two equation differ only in the notation used. C and $\tau $ is the torque, I is the moment of inertia and $\ddot \theta \,and\,\alpha $ refer to angular acceleration. One can again draw comparisons with the linear case (Newton's Second Law) $F = m\ddot s$.

Angular Momentum (Optional)

It's optional to note, but instructive nonetheless that the angular momentum is given by:

\[L = I\dot \theta \]

The reader is encouraged to deduce this by again modelling an object as a matrix of points.

Here I will suggest to the reader a recourse to the second chapter of our mechanics to revise the equations regarding constant angular acceleration.

Ex 1. A flywheel, such that it has a moment of inertia of 300 $kg\,{m^2}$, is rotating at $2\,rad{\kern 1pt} {s^{ - 1}}$. A constant torque of 150 $N{\kern 1pt} m$ is applied to the flywheel for 10 seconds, in the sense that it increases its rate of rotation. Find

a) Angular Velocity at the end of this time

b) Angular Displacement during this time

c) Increase in the Kinetic Energy of the flywheel

Sol.

a) We note to begin with $C = 150;\,I = 300$

From this we have:  $\ddot \theta  = \frac{C}{I} = \frac{{150}}{{300}} = 0.5\,rad{\kern 1pt} {s^{ - 2}}$

The relevant equation then is:

$\omega  = {\omega _0} + \alpha t$

$\omega  = {\omega _0} + \alpha t = 2 + 0.5\left( {10} \right) = 7$

b) The equation to be used here is:

$\theta  = {\theta _0} + {\omega _0}t + {\textstyle{1 \over 2}}\alpha {t^2} = 0 + 2\left( {10} \right) + {\textstyle{1 \over 2}}\left( {0.5} \right)\left( {100} \right) = 45$

c) $RE = {\textstyle{1 \over 2}}I{\omega ^2}$

Increase in RE is then given by:

$\Delta RE = {\textstyle{1 \over 2}}I{\omega ^2} - {\textstyle{1 \over 2}}I{\omega _0}^2 = {\textstyle{1 \over 2}}I\left( {{\omega ^2} - {\omega _0}^2} \right) = {\textstyle{1 \over 2}}300\left( {{7^2} - {2^2}} \right) = 6750$

Further Mechanics | Chapter 3: Equilibrium of a rigid body under coplanar forces

Curriculum Objectives

• understand and use the result that the effect of gravity on a rigid body is equivalent to a single force acting at the centre of mass of the body, and identify the centre of mass by considerations of symmetry in suitable cases;
• calculate the moment of a force about a point in 2 dimensional situations only (understanding of the vector nature of moments is not required); 
• recall that if a rigid body is in equilibrium under the action of coplanar forces then the vector sum of the forces is zero and the sum of the moments of the forces about any point is zero, and the converse of this; 
• use Newton’s third law in situations involving the contact of rigid bodies in equilibrium;
• solve problems involving the equilibrium of rigid bodies under the action of coplanar forces (problems set will not involve complicated trigonometry).

Personally I do not believe there is anything particularly "new" to be taught here. Most, if not all, that you need to know you must already know from courses that are prerequisites to this course. You may not, however, assume that you can safely skip this chapter, for the question set on this topic tend to be more difficult than that you may be comfortable with. I shall for the reason stated leave this page empty, except for posting solutions to some difficult past paper questions.

Further Mechanics | Chapter 2: Circular Motion

Curriculum Objectives

• recall and use the radial and transverse components of acceleration for a particle moving in a circle with variable speed; 


• solve problems which can be modelled by the motion of a particle in a vertical circle without loss of energy (including finding the tension in a string or a normal contact force, locating points at which these are zero, and conditions for complete circular motion).

Introduction

For a body, of mass m, in uniform motion, a constant force, F, applied in the direction of motion will accelerate the body exactly by a measure of $\frac{F}{m}\,m{s^{ - 2}}$. What we wish to achieve here is to talk about the effect forces perpendicular to the motion of a body tend to engender. As such forces wouldn't have a component in the direction of motion, the particle's speed in that direction will remain the same. The particle however will suffer a change in direction. Also note that if the force acts on the body in a direction that is some angle to the direction of motion, but not zero or 90 degree (or any multiple thereof) then, the effect of the body would be to change the direction of the body and change the speed of the body in the direction of motion.

The path the last two bodies in the above consideration will take, will be of a curved nature. We will talk here only of a special curve - the circle. The beginning of our study, as with all beginnings, will be modest. We will first talk of the simpler case of constant speed for a particle in circle, before engaging in the discussion of variable speeds.

Angular Velocity and Acceleration

Before we may embark on the sojourn planned above, we have to cover the concept of angular velocity, and acceleration.

We know by definition that a radian is the angle subtended at the centre by a sector of a segment of the circle, if the curved length of the segment is equal to its radius. Furthermore, we know for any segment, that has a curved length of s, and radius r, the angle subtended at the centre is:

$\theta  =$$ \frac{s}{r}$

Most books usually quote this result without proof and I would have done so as well, until I realised, in my efforts to prove it, that it takes nothing more than you have already learnt in the course. We wish to find a relationship between the radius, angle and arc length. You should recall that we have a formula that links all three in a sense.

$S = \int_\alpha ^\beta  {\sqrt {{{\left( f \right)}^2} + {{\left( {\frac{{df}}{{d\theta }}} \right)}^2}} } \,d\theta $

In polar form a circle has the following form: $f\left( \theta  \right) = R$

Putting this into what we have gotten above:

$S = \int_\alpha ^\beta  {\sqrt {{R^2} + {{\left( 0 \right)}^2}} } \,d\theta  = R\beta  - R\alpha $

Where both $\alpha$ and $\beta$ are angles measured from some fixed axis, the choice of which however is arbitrary. The only conditions we impose on the the angles are $\beta ,\alpha  \ge 0$. Something of the following form:

 Now if one were to set OX, as the fixed axis on the circle, where O is the centre of the circle and X a point on the circumference exactly to the right to the centre. Further if the radius is R, then we can find the arc length AB, by using the definite integral. The matter could be further simplified, if the fixed axis is set at OA. Then the arc length is simply: $A\beta $. Swap out $\beta$ with $\theta$ and you have proven the result.

Now consider the motion of a particle along a circular path. It may either move in one of two directions: clockwise or anticlockwise. For a measure of how large a displacement the particle has gone through we have two options. One is to look at the length of the curved path the particle has followed or the angle the particle has gone through. Both the measures are important. We will talk of the angular measure for displacement, however. This measure is, unsurprisingly, called the angular displacement and denoted by $\Delta \theta $ (some books prefer $\theta $). For discrete cases we have:

$\Delta \theta  =$$ \frac{{\Delta s}}{r}$ 

Here $\Delta s$ is the displacement the particle has gone through. So we see that the displacement the particle goes through is related to the angular displacement; they are proportional.

The concept of angular velocity comes naturally, when we derive analogies from linear motion. As with (instantaneous) velocity, (instantaneous) angular velocity ($\omega $) is the time-derivative of angular displacement. The unit of angular velocity is $rad{\kern 1pt} {s^{ - 1}}$.

$\omega =$$ \frac{{d\theta }}{{dt}}$

Angular acceleration is derived similarly, and is denoted by $\alpha$.

$\alpha  =$$ \frac{{d\omega }}{{dt}} = \frac{{{d^2}\theta }}{{d{t^2}}}$

Of course one could use these differential equations to derive the constant acceleration kinematics you should have mastered by now. For example:

$\alpha  = \frac{{d\omega }}{{dt}} \Rightarrow \int {\alpha \cdot dt}  = \int {d\omega } $

Assuming that the angular acceleration is constant:

$\begin{array}{l} \alpha = \frac{{d\omega }}{{dt}} \Rightarrow \int {a \cdot dt} = \int {d\omega } \\ \alpha \int {dt} = \int {d\omega } \\ \alpha t + {\omega _0} = \omega \end{array}$

Note that ${\omega _0}$ is simply the constant of integration. If we let t equal zero, we find that the constant in this case is the initial angular velocity. Of course ${\omega _0}$ denotes the very same. This is the rotational analogue of the linear one: $v = {v_0} + at$

In the same vein, all the SUVAT equations that you should have learned already, are naturally extended to the rotational case by the simple substitution of the angular acceleration, velocity and displacement for the usual linear quantities. I state them below as a quick reference.

$\begin{array}{l} \omega = {\omega _0} + \alpha t\\ \theta = {\theta _0} + {\omega _0}t + {\textstyle{1 \over 2}}\alpha {t^2}\\ \theta = {\theta _0} + {\textstyle{1 \over 2}}\left( {{\omega _0} + \omega } \right)t\\ {\omega ^2} = {\omega _0}^2 - 2\alpha \left( {\Delta \theta } \right)\\ \theta = {\theta _0} + \omega t - {\textstyle{1 \over 2}}\alpha {t^2} \end{array}$

Here $\omega $ represents the final angular velocity, ${\omega _0}$ represents initial velocity. $\alpha $ represents the final angular acceleration, and ${\alpha _0}$ represents the initial angular acceleration. $\theta $ represents the final angular displacement, and ${\theta _0}$ represents the initial angular displacement. $\Delta \theta  = \theta  - {\theta _0}$
Also note the following relationship between the transversal velocity and acceleration and rotational acceleration:

We know that:

$s = r\theta $

Then by differentiating both sides by the time (twice for acceleration), and taking note of the fact that the radius remains constant we find the following relationship between the magnitudes of the linear or transversal velocity and acceleration and that of angular velocity and acceleration

$\begin{array}{l} \frac{{ds}}{{dt}} = \frac{d}{{dt}}\left( {r\theta } \right) \Rightarrow \frac{{ds}}{{dt}} = r\frac{{d\theta }}{{dt}} \Rightarrow v = r\omega \\ \frac{{dv}}{{dt}} = \frac{d}{{dt}}\left( {r\omega } \right) = r\left( {\frac{{d\omega }}{{dt}}} \right) \Rightarrow a = r\alpha \end{array}$

Motion in a circle with constant speed

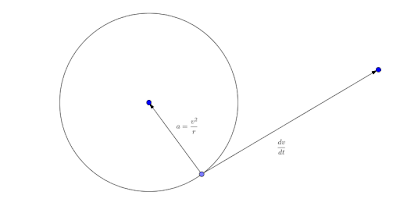
Consider a particle describing a circle, with centre O, radius r, and a constant speed of v. As there is no change in the speed, no force component acts in the direction of the motion, which is tangential at any instant. A simple observation can convince you of the fact. Tie a rubber to a string and bring it into circular. Snap its chord and chart its course. At each point you shall find the rubber to move in the direction of the tangent at that point.

A force must be however acting on it because the direction is changing. The only possible candidates are directions perpendicular to the tangent at a given point. As the particle seems to be revolving around centre as opposed to moving away from it, we conclude that the force is acting towards the centre, or that it is acting along the radius. We call this radial acceleration. Memorise this term, you will be seeing that a lot. 

As a general sketch of the matter, consider:

Having understood the nature of the radial acceleration, it only follows that we would look to quantify it. Let us forsake the proof at the moment (you may find it in the assortment of proofs post), we find that the magnitude of the radial acceleration is given by:

$a = \frac{{{v^2}}}{r}$

As $v = r\omega $

$a = \frac{{{v^2}}}{r} = \frac{{{r^2}{\omega ^2}}}{r} = r{\omega ^2}$

$a = \frac{{{v^2}}}{r} = v \cdot \frac{v}{r} = v\omega $

Ex.

A particle of mass m is attached by a light inextensible string of length l, to a fixed point A on a smooth horizontal surface. If it is travelling with constant angular velocity $\omega$ in a circle what is the tension in the string and the reaction in the table.

We begin with noting that that the particle is moving in horizontal circles, and that there is no vertical component to the acceleration. We may conclude that the vertical forces are in equilibrium. The vertical forces of course are the reaction and the weight. We have then:

$R = mg$

Also note that the force keeping the particle in uniform circular motion is the tension exerted by the string. We compute it by computing the radial acceleration and then applying Newton's second law. We use $a = r{\omega ^2}$ because that is the information given in the question. You could make the necessary substitutions and use any one of the equations.

Hence 

$a = r{\omega ^2} = l{\omega ^2}$

$F = ma = ml{\omega ^2} = T$

For the physics students, this force is called the centripetal force.

Motion in a circle with variable speed

The velocity of a particle travelling on a circular path with varying speed is changing both in magnitude and direction. The particle therefore has two acceleration components:

a) towards the centre of the circle, a component which is the rate of change of direction of the velocity. The magnitude at any given moment as before is $a = \frac{{{v^2}}}{r}$. However v is variable and the acceleration therefore is also, labile. Usually in our questions the velocity will be given as a function of time or displacement.

b) in the direction of motion, i.e. along the tangent to the circle at P, a component $\frac{{dv}}{{dt}}$ which is the rate of change of the magnitude of the velocity.

Motion of this type results in the force having both a radial and tangential component. This situation arises when the particle, (and the circular path) is in a vertical plane. A general sketch of the matter is then of the form:

While motion of this form, considering how it is formed, can be fairly difficult to analyse, in our study we will be working with a particularly simplifying assumption: The velocity of the object after it has begun the motion will not be affected by any other external force except weight. In such cases the mechanical energy is conserved. Having made this assumption we shall find that these motion can be, virtually all the time, studied using three equations, that I shall generalise for you below. 

Allow me to set the problem. we have a small bead of mass m, that is threaded onto a smooth wire in the shape of a circle, with radius r, and centre O. The circle is fixed in a vertical plane and the bead passes the lowest point A (the point directly downwards to the centre) on the wire with a speed of u. It subsequently passes with a speed of v through another point B where the angle BOA is $\theta$. Consider the following:

Note that R stands for the reaction force caused by the wire. By equating the transversal and radial forces we get the following equations (we need to resolve weight into the two components).

Along the radius we have:

$R - mg\cos \theta  = m\frac{{{v^2}}}{r}$

Along the tangent we have:

$mg\sin \theta  =  - m\frac{{dv}}{{dt}}$

The maximum possible value of R occurs at A. This follows from the first equation, as cosine can at most take the value of 1, and at this value the angle that the bead makes is zero (or 360) degree(s).

The third equation we get from the conservation of energy.

u and v are the respective speeds of the body at those positions. As the total mechanical energy will be conserved, we will work out the kinetic and gravitational potential energy at both points, and compare their sums. However there is one caveat before we begin. The gravitational potential energy requires some plane of reference, whereat the gravitational potential is zero. You must be used to using the ground as the point of zero gravitational potential, in this case however there is no ground to be our reference, which forces us to decide on a different one. I have pointed out two possibilities A and B, there are of course infinitely more.

If we let B be the point of zero potential, then the total mechanical energy of the body when it has speed u is:

$ME = {\textstyle{1 \over 2}}m{u^2}$

The mechanical energy at the other point is then:

$ME = {\textstyle{1 \over 2}}m{v^2} + mgr\left( {1 - \cos \theta } \right)$

Then we can say:

${\textstyle{1 \over 2}}m{u^2} = {\textstyle{1 \over 2}}m{v^2} + mgr\left( {1 - \cos \theta } \right)$

I hope I don't have to point out why this equation would be helpful.

If we use A as the point of reference, then we will have to submit to the concept of "negative gravitational potential energy". We shall treat our negative energy as follows: for a body of mass m, at a vertical distance of a, below our zero potential line, the gravitational potential energy is $ - mga$.

Following this convention, the mechanical energy when the body has speed u is:

$ME = {\textstyle{1 \over 2}}m{u^2} - mgr$

For the other body we can say then:

$ME = {\textstyle{1 \over 2}}m{v^2} - mgr\cos \theta $

We conclude then:

${\textstyle{1 \over 2}}m{u^2} - mgr = {\textstyle{1 \over 2}}m{v^2} - mgr\cos \theta $

Use whichever you find easier, as we see regardless of the choice of the line of reference, we get equivalent equations.

The case we began studying was such that a bead was threaded on a smooth wire, however this form of analysis is valid for a variety of different yet fundamentally similar situations:

1) A particle attached to one end of a light rod which is free to rotate about a smooth fixed axis through the other end. In this case everything remains the same, however there is no reaction force involved here in its stead there is the stress in the rod. So if you were to replace R by that force, let us say F, then the equations hold here as well.

2) A particle rotating on the inside of a smooth circular surface. Here the equations can be used verbatim.

3) A particle rotating at the end of a light string whose other end is fixed. Here replace the reaction force by the tension in the string and the equations are again usable.

However there is one case that you should be aware of, whose treatment has to be adapted from what we have already established. 

4) A particle that is moving on the surface of a smooth circular surface. This case is different because the reaction force here is acting away from the centre. Only weight can provide any centripetal force and that too only in the upper hemisphere. So the particle will stay in contact with top of the circle only. The case is as follows, and the equations need only be slightly modified.

The equations are then:

$mg\cos \theta  - R = \frac{{m{v^2}}}{r}$

$mg\sin \theta  = m\frac{{dv}}{{dt}}$

By the conservation of mechanical energy, we have:
${\textstyle{1 \over 2}}m{u^2} + mgr = {\textstyle{1 \over 2}}m{v^2} + mgr\cos \theta $

Where u is the speed of the particle directly above the centre and v at some subsequent point.

Ex.

A particle of mass 2 kg is attached to the end B of a light rod AB of length 0.8m which is free to rotate in a vertical plane about the end A. If the end B, when vertically below A, is given a horizontal velocity of 3 metres per second show that the particle will not describe complete circles. Find the angle through which it oscillates and the greatest possible stress in the rod during the motion.

Sol:

The best way to approach these question is to draw a model to study. Using the information given above we have the following:

Now we apply our equations to solve the question. We wish to show that the particle doesn't describe full circle, and begins oscillating. For this it would be sufficient to show that there is a point, between the angles 0 and 180 (ask yourself why don't consider the range between 180 and 360), that the particle comes to rest. We have the initial and final velocities (3 and 0), so we should use that equation that involves both of these quantities. We have then (Note that the horizontal line where the PE is zero, passes through the origin):

${\textstyle{1 \over 2}} \cdot 2 \cdot {3^2} - 2g\left( {0.8} \right) = {\textstyle{1 \over 2}} \cdot 2 \cdot {0^2} - 2g\left( {0.8} \right)\cos \theta $

$ \Rightarrow \cos \theta  = 0.425 \Rightarrow \theta  = {64.8^ \circ }$

So the angle that the particle oscillates through is twice this angle. It only remains to find the maximum stress. We use the first of our equations because it involves centripetal force.

$T - 2g\cos \theta  = \frac{{2 \cdot {v^2}}}{{0.8}}$

Obviously T is greatest when $\theta  = {0^ \circ };v = 3$

The maximum tension then is given by: $\left( {\frac{{18}}{{0.8}} + 2g} \right)N = 42.1\,N$

Note that N is the unit not any variable.

Further Mechanics | Chapter 1: Momentum and Impulse

Curriculum Objective

• recall and use the definition of linear momentum, and show understanding of its vector nature (in one dimension only);
• recall Newton’s experimental law and the definition of the coefficient of restitution, the property 0 ø e ø 1, and the meaning of the terms ‘perfectly elastic’ (e = 1) and ‘inelastic’ (e = 0);
• use conservation of linear momentum and/or Newton’s experimental law to solve problems that may be modelled as the direct impact of two smooth spheres or the direct or oblique impact of a smooth sphere with a fixed surface;
• recall and use the definition of the impulse of a constant force, and relate the impulse acting on a particle to the change of momentum of the particle (in one dimension only)

Introduction

In Classical Mechanics there exists a quantity called Linear Momentum associated with an object that is defined as the product of the mass and the velocity of the body. Which is to say:

\[\bar p = m\bar v\]

Note that momentum, like velocity, is a vector quantity, hence has a magnitude and a direction associated with it. In a more formal treatment the momentum in the above equation (and the velocity) would be a three dimensional vector, however in this course, you will not be required to work in more than two dimensions.

The physical interpretation of this quantity is the ability of body to retain its velocity. A massive truck moving at the same speed as a sedan, would required a greater force, or more time to be brought to a halt, while the sedan would be comparatively easier to be brought to rest.

Ex.

Given that two bodies, of masses 10 and 6 kg, are moving at the velocities of $6\;m{s^{ - 1}}$ and $12\;m{s^{ - 1}}$ respectively. Calculate their momentum and hence use it to predict which body will come to rest quicker if the same force is applied as resistance to the bodies. 

Sol:

The momentum of the bodies respectively are:

$\begin{array}{l} {p_1} = {m_1}{v_1} = 10 \cdot 6 = 60\;kgm{s^{ - 1}}\\ {p_2} = {m_2}{v_2} = 6 \cdot 12 = 72\;kgm{s^{ - 1}} \end{array}$


By the reasoning already stated above, we conclude the body with greater momentum will take more time to be brought to rest.

Working from Newton's Second Law of Motion, we know that:

\[F = ma = m\frac{{dv}}{{dt}}\]

As we will only be working with discrete changes in momentum, we may do away with the infinitesimal changes and the use of calculus and we may simply denote it as:

\[F = m\frac{{\Delta v}}{{\Delta t}} = \frac{{\Delta \left( {mv} \right)}}{{\Delta t}} = \frac{{\Delta p}}{{\Delta t}}\] where $\Delta$ denotes the change in the quantity. Even though we have forgone calculus, you can see how the treatment wouldn't be much different even if we were working with the derivative.

We conclude then that the rate of change in the momentum is equal to the resultant force acting on the particle.

Further note that this gives us a new unit for the momentum, the Newton-second. We see that the change in time multiplied by force is equal to the change in momentum. As the units of change in a quantity are same as those of the quantity itself, we can conclude safely that momentum can indeed be measured in Newton-Seconds.

As we study discrete changes in momentum, consider the following:

\[F \cdot \Delta t = \Delta \left( {mv} \right) = m{v_f} - m{v_i}\]

The change in momentum is ofttimes an important quantity in our study, hence we give it a special name. The Impulse produced by a force is equal to the change in momentum it causes. We note that its units are Ns, same as momentum, and I denote it with $\varphi $, but I am not sure what your examiner prefers. It would be advisable to define every variable you use in the paper for that very reason. 


Ex. 

A truck of mass 1000 kg travelling at 3 metres per second is brought to rest when it hits a buffer in 2 seconds. What force (assumed to be constant) is exerted by the buffer?

Sol. 

$\begin{array}{l} \varphi = m{v_f} - m{v_i} = 0 - 1000\left( { - 3} \right) = 3000\\ \varphi = Ft = 3000\\ t = 2 \Rightarrow F = 1500\,N \end{array}$

Conservation of Momentum

We know already:

$F = \frac{{dp}}{{dt}}$

Hence if there is no external resultant force, F, the change in momentum for a single body will be zero. Naturally after a single body, we talk about a collection of bodies. 

Of a collection of bodies, or a closed system, we note that by the equation given above without an external force acting on the system there will be no change in the momentum. Of course this doesn't cover the interaction between any bodies in the closed system. We also have to consider the effect of the interaction of the bodies in the closed system with each other.

Let us say that two bodies in a closed system interact in some manner, say collide. We call the objects A and B, assume they comprise the entire system for the moment, and further call the force A exerts on B $F_{AB}$ and the force B exerts on A $F_{BA}$. We know from Newton's third law that:

$F_{AB}=-F_{BA}$

$\frac{dp_{B}}{dt}=-\frac{dp_{A}}{dt}$

$\frac{d}{dt}\left (p_{A}+p_{B}  \right )=0$

We see then that despite the fact that the momentum of the bodies has changed, the momentum of the entire closed system remains the same. For more than two bodies you can easily adapt this argument.

We call this the law of conservation of momentum.

Newton's Law of Restitution

We begin with defining an elastic and inelastic collision. An elastic collision is such that when two objects collide, they bounce back. If however they coalesce after the collision, the impact is inelastic. 

For those studying Physics, you must be familiar of the terms, but defined in the context of Kinetic Energy. Different while they may seem, they don't contradict one another, rather suggest much the same thing.

It is generally held that if after a collision the two objects do bounce back, the separation speed (the speed after the collision) will be equal or less than the approach speed (speed ere collision). Experimental evidence suggests that the ratio of these relative speeds is constant. This is known as the Newton's Law of Restitution. It may be written as follows:

\[\frac{{relative\,separation\,speed}}{{relative\,approach\,speed}} = e\]

"e" is then called the coefficient of restitution and it is constant for particular objects. We also note that it must be restricted to $0 \le e \le 1$ ($e > 1$ may also occur but you need not worry about that). This law holds both for two moving objects, and one moving and one fixed object, the law of conservation of momentum however holds for only the first case (why?).

In this range, consider how e can take the values 0 and 1 in particular. 0 may occur when the collision is inelastic, for if it is inelastic then the objects coalesce and move at the same speed together, hence rendering the relative separation speed zero. 1 happens in the special case called a perfectly elastic collision, wherein the particle retain all their Kinetic Energy, and thereby have the same separation speed as approach speed.

This being a mathematical course you are going to need a more mathematically grounded formula rather than the vague concept of relative approach or separation speed. Note then that the coefficient of restitution is given by:

$\frac{{{v_b} - {v_a}}}{{{u_a} - {u_b}}}$ $= e$

Here we call the two objects a and b. Then ${v_b},{v_a}$ are the velocities of b and a after collision and ${u_b},{u_a}$ are the velocities of the objects b and a before the collision

Also note that for an object that collides with a surface the coefficient of restitution becomes:

$ e =$ $\frac{{{v_a}}}{{{u_a}}}$

Where we have called the object a, and the surface b, and plugged in the values zero for the value. A further consideration that eliminates the negative sign is that $v_a$ is in the opposite direction as $u_a$.

Ex.

Two identical smooth spheres A and B are free to move on a horizontal plane. B is at rest and A is projected with velocity $u$ to strike B directly. B then collides with a vertical wall that is perpendicular to the direction of the motion of the spheres. After rebounding from the wall B again collides with A and is brought to rest by this impact. If the coefficient of restitution has the same value for all the impacts, prove that $e=1$.

Sol.

In this question and all the question of this form that the examiner may ask you, there will be a multitude of variables. You must keep strict track of them, perhaps making a proper note in the beginning and any relationship or special conditions as given in the question. For this question I have:

1) $u$ as given in the question is the initial speed of A before collision

2) $u_1$ and $v_1$ are the speeds of A and B respectively after the first collision

3) $v_2$ is the speed of B after it has rebounded from the wall

4) $u_3$ is the speed of A after the final collision between B and A

The manner I suggest to do this in, would be to assign to every different body a different letter, and then the index would tell you what collision the velocity is consequent to. For example $u_3$ would be the velocity of the Sphere A after the third impact.

Also, note that I said speed, because the direction of the motion make a difference here. Consider two balls approaching one another, then the relative approach speed would be the sum of their speeds, if both are moving in the same direction than it would be the difference. Both of which cases are simply the difference of their velocities. While for calculations velocities would have sufficed, in analysis questions such as these we must need to use the difference in the direction of motion.

First collision

By the Law of Restitution:

$eu = {v_1} - {u_1}$

By the Law of Conversation of Momentum

$mu = m{u_1} + m{v_1} \Rightarrow u = {u_1} + {v_1}$

It follows that:

$\left( {1 + e} \right)u = 2{v_1}$

$\left( {1 - e} \right)u = 2{u_1}$

Second Collision

By Law of Restitution:

$e{v_1} = {v_2}$

Note that the momentum will not be conserved here because there is an external force at work here, that is keeping the vertical wall from moving. Recall that the Law of Conservation of Momentum doesn't hold when there is an external impetus.

Third Collision

By Law of Restitution:

$e\left( {{u_1} + {v_1}} \right) = {u_3}$ 

Here the direction of approach matters; as the spheres are approaching one another the relative approach speed is the sum of their speed, which would be of course the difference of their velocities.

By Conservation of Momentum:

${v_2} - {u_1} = {u_3}$

Eliminating $u_3$ gives:

${v_2} - {u_1} = e\left( {{u_1} + {v_2}} \right) \Rightarrow {v_2}\left( {1 - e} \right) = {u_1}\left( {1 + e} \right)$

Using previous equations we have built, we can create expressions dependent only on u and e for $u_1$ $u_2$, and then put them into the above equation.

${v_2} = e{v_1} = e\left( {{\textstyle{1 \over 2}}u} \right)\left( {1 + e} \right)$

${u_1} = \left( {1 - e} \right)\left( {{\textstyle{1 \over 2}}u} \right)$

$e\left( {1 + e} \right)\left( {{\textstyle{1 \over 2}}u} \right)\left( {1 - e} \right) = \left( {1 - e} \right)\left( {{\textstyle{1 \over 2}}u} \right)\left( {1 + e} \right)$

Make the necessary eliminations and our question is solved.

Consider the following example from your past papers (Oct/Nov 2014 Paper 21 Q1)


a) Two smooth spheres A and B, of equal radii and masses 2m and m respectively, lie at rest on a smooth horizontal table. The spheres A and B are projected directly towards each other with speeds 4u and 3u respectively. The coefficient of restitution between the spheres is e. Find the set of values of e for which the direction of motion of A is reversed in the collision.

Sol:

1) $v_A$ be the velocity of sphere A after the collision an $v_B$ the velocity of B after the collision.

We assume that sphere A is moving in the positive direction and B is moving in the negative direction. They have the velocities: 4u; and -3u. 

By Conservation:

\[2m\left( {4u} \right) + m\left( { - 3u} \right) = 2m{v_A} + m{v_B} \Rightarrow 8u - 3u = 2{v_A} + {v_B} = 5u\]

By restitution:

\[\frac{{{v_A} - {v_B}}}{{{u_B} - {u_A}}} = \frac{{{v_A} - {v_B}}}{{ - 3u - 4u}} = e\]
\[{v_A} - {v_B} =  - 7eu\]


We are concerned with the motion of the Sphere A, hence we use the above system to find a value for it. With the necessary algebra, you will find that:

\[{v_A} = {\textstyle{1 \over 3}}\left( {5 - 7e} \right)u\]

As by assumption $u > 0$, for the sphere to change direction $v_A$ must be less than zero. Now, by equality, ${\textstyle{1 \over 3}}\left( {5 - 7e} \right)u < 0$. As $u > 0$:

${\textstyle{1 \over 3}}\left( {5 - 7e} \right) < 0 \Rightarrow e > {\textstyle{5 \over 7}}$ 

We conclude: $e \in \left( {{\textstyle{5 \over 7}},1 } \right]$

Oblique collision with a surface

We have covered direct impact between moving spheres, and between one moving sphere and a surface. All that is left is oblique impact with a surface. 

Oblique impact is such that the sphere collides with the surface at an angle. In this case, the problem is no longer a one-dimensional one, but rather a two dimensional one. Hence, as with studying projectile motion, we will resolve the velocity in two different, perpendicular components. Our choice of the components is such that the direction of impact (the normal to the surface) is one and the other then has to be parallel to the surface. For example consider:

 

After the collision the component parallel to the surface will remain the same, i.e. $V\sin (x)$, assuming that the ball bounces back without sliding across the surface. In the line of impact ($V\cos (x)$), however the law of restitution will hold and as before separation speed = e * approach speed.

Consider the following past paper question. (Oct/Nov 14 Paper 21 Q2)

Sol:

Let us begin with the easier parallel component. Initially it is at $4\cos (\alpha )$. Let $\beta$ be the angle that P makes with the horizontal when it bounces back. We know the speed of P is halved, hence 2, and that the parallel component remains constant. Hence:

$4\cos (\alpha ) = 2\cos\left( \beta  \right)$

The normal component then gives us:

$0.4 \cdot 4\sin (\alpha ) = 2sin\left( \beta  \right)$

We wish to find $\alpha$

We know:

${V^2} = {2^2} = {V^2}{\sin ^2}\beta  + {V^2}{\cos ^2}\beta  = {\left( {1.6\sin \alpha } \right)^2} + {\left( {4\cos \alpha } \right)^2}$

Beyond this it is only the matter of using ${\sin ^2}\theta  + {\cos ^2}\theta  = 1$ to create a quadratic involving either sine or cosine, and thence finding $\alpha$. You should find that:

$\alpha  = 1.24$